Code
%matplotlib widget
import numpy as np
from eomaps import Maps
from tuw_education_notebooks.view_bayes_flood import view_bayes_flood
from tuw_education_notebooks.calc_bayes_flood import sig0_dc, calc_likelihoods1 Reverend Bayes aktualisiert unser Glauben an Flood Detection
Wie eine 275 Jahre alte Idee hilft, das Ausmaß von Überschwemmungen zu kartieren
1.1 Von der Rückstreuung zur Hochwasserkartierung
In diesem Notebook wird erklärt, wie die Rückstreuung von Mikrowellen (\(\sigma^0\)) (Abbildung 1.1) verwendet werden kann, um das Ausmaß eines Hochwassers zu kartieren. Wir replizieren in dieser Übung die Arbeit von Bauer-Marschallinger u. a. (2022) über den Bayesian-basierten Hochwasserkartierungsalgorithmus der TU Wien.
In den folgenden Zeilen erstellen wir eine Karte mit EOmaps (Quast, o. J.) der \(\sigma^0\) Rückstreuwerte.
Code
m = Maps(ax=121, crs=3857)
m.set_data(data=sig0_dc, x="x", y="y", parameter="SIG0", crs=Maps.CRS.Equi7_EU)
m.plot_map()
m.add_colorbar(label="$\sigma^0$ (dB)", orientation="vertical", hist_bins=30)
m.add_scalebar(n=5)
m2 = m.new_map(ax=122, crs=3857)
m2.set_extent(m.get_extent())
m2.add_wms.OpenStreetMap.add_layer.default()
m.apply_layout(
{
'figsize': [7.32, 4.59],
'0_map': [0.05, 0.18, 0.35, 0.64],
'1_cb': [0.8125, 0.1, 0.1, 0.8],
'1_cb_histogram_size': 0.8,
'2_map': [0.4375, 0.18, 0.35, 0.64]
}
)
m.show()1.2 Mikrowellenrückstreuung über Land und Wasser
Reverend Bayes befasste sich mit zwei Ereignissen, von denen das eine (die Hypothese) vor dem anderen (dem Beweis) eintrat. Wenn wir die Ursache kennen, ist es leicht, logisch auf die Wahrscheinlichkeit einer Wirkung zu schließen. In diesem Fall wollen wir jedoch die Wahrscheinlichkeit einer Ursache aus einer beobachteten Wirkung ableiten, auch bekannt als “umgekehrte Wahrscheinlichkeit”. Im Fall der Hochwasserkartierung haben wir \(\sigma^0\) Rückstreuungsbeobachtungen über Land (die Wirkung), und wir wollen die Wahrscheinlichkeit von Überflutung (\(F\)) und Nicht-Überflutung (\(NF\)) ableiten.
Mit anderen Worten, wir wollen die Überflutungswahrscheinlichkeit \(P(F)\) bei einem Pixel mit \(\sigma^0\) wissen:
\[P(F|\sigma^0)\]
und die Wahrscheinlichkeit, dass ein Pixel nicht überflutet wird \(P(NF)\) bei einem bestimmten \(\sigma^0\):
\[P(NF|\sigma^0).\]
Bayes zeigte, dass diese aus der Beobachtung abgeleitet werden können, dass die Vorwärts- und Rückwärtswahrscheinlichkeit gleich sind, so dass:
\[P(F|\sigma^0)P(\sigma^0) = P(\sigma^0|F)P(F)\]
und
\[P(NF|\sigma^0)P(\sigma^0) = P(\sigma^0|NF)P(NF).\]
Die Vorwärtswahrscheinlichkeit von \(\sigma^0\) für das Auftreten von Überschwemmungen (\(P(\sigma^0|F)\)) und \(\sigma^0\) für das Ausbleiben von Überschwemmungen (\(P(\sigma^0|NF)\)) lässt sich aus früheren Informationen über die Rückstreuung über Land- und Wasserflächen ableiten. Wie in der folgenden Skizze (Abbildung 1.2) zu sehen ist, unterscheiden sich die Eigenschaften der Rückstreuung über Land und Wasser erheblich.
1.3 Likelihoods
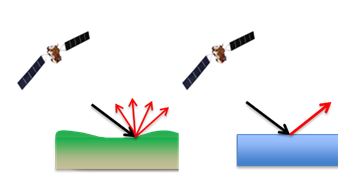
Die so genannten Likelihoods von \(P(\sigma^0|F)\) und \(P(\sigma^0|NF)\) lassen sich also aus den Rückstreuungsinformationen der Vergangenheit berechnen. Ohne auf die Einzelheiten der Berechnung dieser Wahrscheinlichkeiten einzugehen, kann man auf ein Pixel der Karte klicken, um die Wahrscheinlichkeiten für \(\sigma^0\) für Land oder Wasser darzustellen.
Code
view_bayes_flood(sig0_dc)1.4 Posterioren
Nach der Berechnung der Likelihoods können wir nun die Wahrscheinlichkeit des (Nicht-)Flutens eines Pixels mit \(\sigma^0\) berechnen. Diese so genannten Posterioren benötigen eine weitere Information, wie aus der obigen Gleichung ersichtlich ist. Wir benötigen die Wahrscheinlichkeit, dass ein Pixel überflutet \(P(F)\) oder nicht überflutet \(P(NF)\) ist. Das sind natürlich die Zahlen, die wir schon die ganze Zeit zu finden versuchen. Wir haben sie aber noch nicht, was können wir also tun? In der Bayes’schen Statistik können wir einfach mit unserer besten Schätzung beginnen. Diese Vermutungen werden als “Prioren” bezeichnet, weil sie die Überzeugungen sind, die wir vor der Betrachtung der Daten haben. Diese subjektive Vorannahme ist die Grundlage der Bayes’schen Statistik, und wir verwenden die soeben berechneten Likelihoods, um unseren Glauben an diese bestimmte Hypothese zu aktualisieren. Diese aktualisierte Überzeugung wird als “Posterior” bezeichnet.
Nehmen wir an, unsere beste Schätzung für die Wahrscheinlichkeit, dass ein Pixel überflutet oder nicht überflutet wird, ist 50:50: ein Münzwurf. Wir können nun auch die Rückstreuungswahrscheinlichkeit \(P(\sigma^0)\) als gewichteten Durchschnitt der Wasser- und Landwahrscheinlichkeiten berechnen, um sicherzustellen, dass unsere Posterioren zwischen 0 und 1 liegen.
Der folgende Codeblock zeigt, wie wir die Prioritäten berechnen.
Code
def calc_posteriors(water_likelihood, land_likelihood):
evidence = (water_likelihood * 0.5) + (land_likelihood * 0.5)
return (water_likelihood * 0.5) / evidence, (land_likelihood * 0.5) / evidenceWir können die Posterior-Wahrscheinlichkeiten für Überflutung und Nicht-Überflutung erneut darstellen und mit dem gemessenen \(\sigma^0\) des Pixels vergleichen. Man kann auf ein Pixel klicken, um die Posterior-Wahrscheinlichkeit zu berechnen.
Code
view_bayes_flood(sig0_dc, calc_posteriors)1.5 Klassifizierung von Überschwemmungen
Nun können wir all diese Informationen kombinieren und die Pixel anhand des Rückstreuungswerts jedes Pixels nach der Überflutungswahrscheinlichkeit klassifizieren. Hier schauen wir nur, ob die Wahrscheinlichkeit einer Überflutung höher ist als die einer Nicht-Überflutung:
Code
def bayesian_flood_decision(id, sig0_dc):
nf_post_prob, f_post_prob = calc_posteriors(*calc_likelihoods(id, sig0_dc))
return np.greater(f_post_prob, nf_post_prob)Man kann auf einen Punkt in der Karte unten klicken, um die Likelihoods und Posterior-Verteilungen (in den linken Subplots) zu sehen.
Code
view_bayes_flood(sig0_dc, calc_posteriors, bayesian_flood_decision)