11 Validation of Remotely Sensed Soil Moisture – Earth Observation Datascience

Comparing H SAF ASCAT soil moisture estimates with in-situ sensors

11.1 Overview

The aim of this notebook is to demonstrate and teach a workflow for validating ASCAT H SAF soil moisture data, sampled at 6.25\(\,\)km distances, using in-situ sensors strategically placed in Mozambique. Validation in this context assesses how well satellite-derived data aligns with the temporal patterns of in-situ measurements. Remember, temporal dynamics are also crucial for anomaly detection in soil moisture records, which in turn affects our ability to monitor droughts (as discussed in the previous notebook). Such validation processes help ensure the accuracy and reliability of weather data, essential for forecasting, climate research, and decision-making. By comparing different datasets, you can identify and address any inconsistencies, thereby improving the quality of meteorological records.

11.2 Imports

import folium
import hvplot
import hvplot.pandas  # noqa
import pandas as pd

11.3 In-situ Soil Moisture

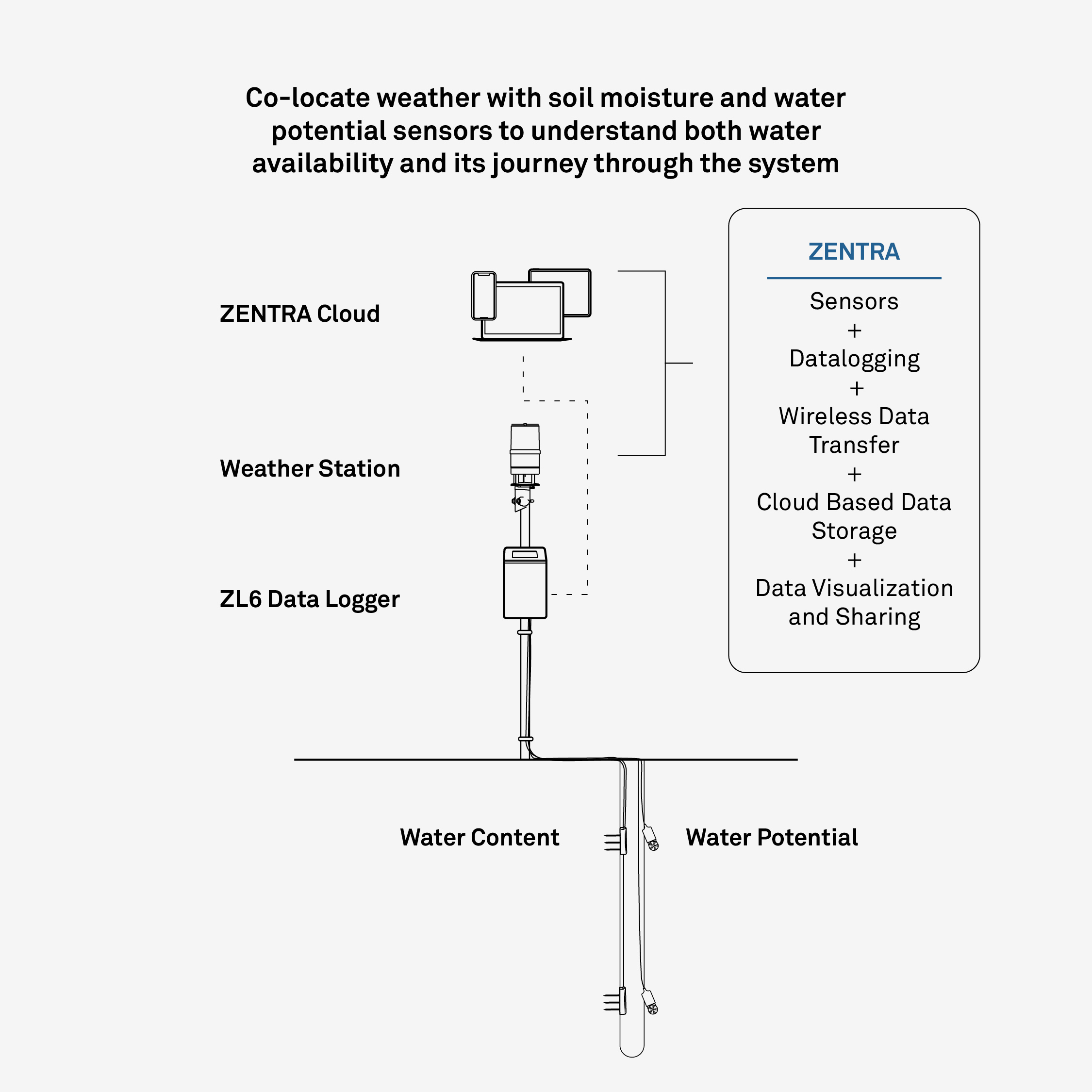
During the DrySat project we have placed 5 in-situ measuring stations (METER™, see image at the top) at strategic locations in Mozambique (Buzi, Chokwé, Mabalane, Mabote and Muanza). The locations are plotted on the following map for reference.

locations = {
    "Muanza": {"latitude": -18.9064758, "longitude": 34.7738921},
    "Chokwé": {"latitude": -24.5894393, "longitude": 33.0262595},
    "Mabote": {"latitude": -22.0530427, "longitude": 34.1227842},
    "Mabalane": {"latitude": -23.4258788, "longitude": 32.5448211},
    "Buzi": {"latitude": -19.9747305, "longitude": 34.1391065},
}


map = folium.Map(
    max_bounds=True,
    zoom_start=6,
    location=[-20, 34],
    scrollWheelZoom=False,
)

for i, j in locations.items():
    folium.Marker(
        location=[j["latitude"], j["longitude"]],
        popup=i,
    ).add_to(map)
map

Make this Notebook Trusted to load map: File -> Trust Notebook

These 5 stations each have 4 in-situ soil moisture sensors (Campbell Scientific™ HydroSense II with CS659) installed at depth intervals of 5, 10, 15, and 30\(\,\)cm. The soil moisture content is measured every 15 minutes and directly stored in the cloud. Since their installation at the end of September 2023, these stations have continually gathered data. For this exercise, we have already cleaned and reformatted a portion of this dataset, which now includes only the measurements from the 5\(\,\)cm depth interval. Please consult us if you need access to the entire raw dataset.

We load the data again as a pandas dataframe, like so:

%run ./src/download_path.py

df_insitu = pd.read_csv(
    make_url("insitu_ssm_timeseries.csv"),  # noqa
    index_col="time",
    parse_dates=True,
)
df_insitu.head()

https://git.geo.tuwien.ac.at/api/v4/projects/1266/repository/files/insitu_ssm_timeseries.csv/raw?ref=main&lfs=true

	name	type	surface_soil_moisture	unit
time
2023-09-30 22:00:00	Buzi	in-situ	0.106400	m³/m³
2023-09-30 22:15:00	Buzi	in-situ	0.106434	m³/m³
2023-09-30 22:30:00	Buzi	in-situ	0.106400	m³/m³
2023-09-30 22:45:00	Buzi	in-situ	0.106434	m³/m³
2023-09-30 23:00:00	Buzi	in-situ	0.106400	m³/m³

Now let’s load the H SAF SSM 6.25\(\,\)km as we did in the previous notebook. But now we filter for the date range to include only dates that contain both ASCAT and in-situ measurements.

RANGE = ("2023-10-01", "2025-05-01")
df_ascat = pd.read_csv(
    make_url("ascat-6_25_ssm_timeseries.csv"),  # noqa
    index_col="time",
    parse_dates=True,
)
mask = (df_ascat.index > RANGE[0]) & (df_ascat.index <= RANGE[1])
df_ascat = df_ascat[mask]
df_ascat.head()

https://git.geo.tuwien.ac.at/api/v4/projects/1266/repository/files/ascat-6_25_ssm_timeseries.csv/raw?ref=main&lfs=true

	name	type	surface_soil_moisture	unit
time
2023-10-01 06:29:06.317000192	Chokwé	ascat	54.97	%
2023-10-01 07:21:28.896999936	Chokwé	ascat	46.66	%
2023-10-01 18:55:21.116000256	Chokwé	ascat	53.92	%
2023-10-01 19:47:51.542999552	Chokwé	ascat	46.14	%
2023-10-03 06:40:10.431000064	Chokwé	ascat	45.05	%

Note, that the units of the in situ measurements differ when compared to the H SAF ASCAT SSM data. The in-situ sensors record soil moisture in volumetric units as cubic meters of water per cubic meters of soil [m\(^3\) / m\(^3\)]. By contrast, the satellite derived estimates are presented as the degree of saturation in the pore spaces of the measured soil.

11.4 Degree of Saturation vs. Volumetric Soil Water Content

To enable a comparison of both data sources, we will first convert the degree of saturation used in the H SAF ASCAT dataset to volumetric units. This will allow us to compare the satellite-derived estimates with the measurements from the in-situ sensors. To achieve this, we need to know the porosity of the soil at the sensor locations. If the porosity is unknown, we can estimate it using a fixed particle density and the location-specific bulk density, as shown in the following expression.

\[ \text{Porosity} = 1 - \frac{\rho_{\text{bulk}}}{\rho_{\text{particle}}} \]

\[ \begin{aligned} \text{Porosity} &\quad \text{: Total pore space in the soil (-)} \\ \rho_{\text{bulk}} &\quad \text{: Bulk density (in g/cm³)} \\ \rho_{\text{particle}} &\quad \text{: Particle density (in g/cm³)} \\ \end{aligned} \]

For your convenience, we have obtain the location-specific bulk density for our targeted areas in Mozambique from SoilGrids. The particle density is typically averaged at about 2.65 g/cm³¹.

density_df = pd.DataFrame(
    {
        "name": ["Buzi", "Chokwé", "Mabalane", "Mabote", "Muanza"],
        "bulk_density": [1.25, 1.4, 1.4, 1.35, 1.25],
    }
).set_index("name")
density_df

	bulk_density
name
Buzi	1.25
Chokwé	1.40
Mabalane	1.40
Mabote	1.35
Muanza	1.25

We can now calculate the soil porosity from the bulk and particle density using the pandas apply method. After that, we will rename the column to “porosity”.

def calc_porosity(x):
    return 1 - x / 2.65


porosity_df = density_df.apply(calc_porosity).rename(
    columns={"bulk_density": "porosity"}
)
porosity_df

	porosity
name
Buzi	0.528302
Chokwé	0.471698
Mabalane	0.471698
Mabote	0.490566
Muanza	0.528302

Now we have the necessary information to convert the H SAF ASCAT SSM to volumetric units by using the following equation.

\[ \text{SSM}_{\text{abs}} = \text{Porosity} \cdot \frac{\text{SSM}_{\text{rel}}}{100} \]

\[ \begin{aligned} \text{SSM}_{\text{abs}} &\quad \text{: Absolute soil moisture, how much of the total soil volume is water (in m³/m³)} \\ \text{SSM}_{\text{rel}} &\quad \text{: Relative soil moisture (in \%)} \end{aligned} \]

To apply this conversion to the HSAF dataset, we will first join the porosity values to the Soil Moisture (SSM) values based on the location names using a method called a left join.

df_ascat_porosity = df_ascat.merge(porosity_df, left_on="name", right_index=True)
df_ascat_porosity.head()

	name	type	surface_soil_moisture	unit	porosity
time
2023-10-01 06:29:06.317000192	Chokwé	ascat	54.97	%	0.471698
2023-10-01 07:21:28.896999936	Chokwé	ascat	46.66	%	0.471698
2023-10-01 18:55:21.116000256	Chokwé	ascat	53.92	%	0.471698
2023-10-01 19:47:51.542999552	Chokwé	ascat	46.14	%	0.471698
2023-10-03 06:40:10.431000064	Chokwé	ascat	45.05	%	0.471698

We can again use the pandas apply method to convert the units.

def deg2vol(df):
    return df.loc["porosity"] * df["surface_soil_moisture"] / 100


df_ascat_vol = df_ascat.copy()
df_ascat_vol["unit"] = "m³/m³"
df_ascat_vol["surface_soil_moisture"] = df_ascat_porosity.apply(deg2vol, axis=1)
df_ascat_vol.head()

	name	type	surface_soil_moisture	unit
time
2023-10-01 06:29:06.317000192	Chokwé	ascat	0.259292	m³/m³
2023-10-01 07:21:28.896999936	Chokwé	ascat	0.220094	m³/m³
2023-10-01 18:55:21.116000256	Chokwé	ascat	0.254340	m³/m³
2023-10-01 19:47:51.542999552	Chokwé	ascat	0.217642	m³/m³
2023-10-03 06:40:10.431000064	Chokwé	ascat	0.212500	m³/m³

11.5 Validation by Visual Inspection

The first step is to visually compare the time series. Visual inspection is essential for ensuring the validity and reliability of your results. It helps identify patterns and trends that might not be evident from data tables. Additionally, it is crucial for detecting outliers, which could indicate sensor malfunctions or data entry errors. In our case, we aim to see if both the in-situ and ASCAT soil moisture data accurately reflect the characteristic seasonal rains of Mozambique.

To facilitate a clear overview, we will first concatenate the two datasets as follows:

df = pd.concat([df_insitu, df_ascat_vol])
df.head()

	name	type	surface_soil_moisture	unit
time
2023-09-30 22:00:00	Buzi	in-situ	0.106400	m³/m³
2023-09-30 22:15:00	Buzi	in-situ	0.106434	m³/m³
2023-09-30 22:30:00	Buzi	in-situ	0.106400	m³/m³
2023-09-30 22:45:00	Buzi	in-situ	0.106434	m³/m³
2023-09-30 23:00:00	Buzi	in-situ	0.106400	m³/m³

Next, we will use the hvplot extension for pandas to create interactive scatter plots for the time series.

df.hvplot.scatter(
    x="time",
    y="surface_soil_moisture",
    by="type",
    groupby="name",
    frame_width=800,
    padding=(0.01, 0.1),
    alpha=0.5,
)

These plots already assure us that the trends in both data records align with the monotonic patterns characteristic of soil wetting during Mozambique’s rainy season.

11.6 Quantitative Validation Metrics

We can now move to a more quantitative estimate. Correlation analysis is a valuable tool for validating meteorological records by comparing different datasets to ensure consistency and accuracy. It measures the strength and direction of the relationship between two variables. In the context of meteorological records, it helps assess how well different datasets align with each other, serving as a quality assurance measure.

Before applying correlation analysis, we need to reshape our dataframe by pairing the data to the same timestamps for each of the five locations. For this, we will use the groupby method in combination with the resample method. The resample method will adjust the time index to a new frequency of 1 day, using the median value to downsample the frequencies from hourly to daily for both ASCAT and in-situ sensor data.

df_insitu_daily = (
    df_insitu.groupby("name")["surface_soil_moisture"]
    .resample("D")
    .median()
    .to_frame("in-situ")
)

df_ascat_vol_daily = (
    df_ascat_vol.groupby("name")["surface_soil_moisture"]
    .resample("D")
    .median()
    .to_frame("ascat")
)

df_combined = pd.merge(
    df_ascat_vol_daily, df_insitu_daily, left_index=True, right_index=True
)
df_combined.head()

		ascat	in-situ
name	time
Buzi	2023-10-01	0.068072	0.110634
	2023-10-02	NaN	0.111050
	2023-10-03	0.048498	0.113430
	2023-10-04	NaN	0.113988
	2023-10-05	0.067623	0.113479

The data is now ready for correlation analysis. For time series analysis, if you’re looking at trends and expect a linear relationship, Pearson correlation is straightforward and precise method.

df_combined.groupby("name").corr(method="pearson")

		ascat	in-situ
name
Buzi	ascat	1.000000	0.664800
Buzi	in-situ	0.664800	1.000000
Chokwé	ascat	1.000000	0.647629
Chokwé	in-situ	0.647629	1.000000
Mabalane	ascat	1.000000	0.729674
Mabalane	in-situ	0.729674	1.000000
Mabote	ascat	1.000000	0.610378
Mabote	in-situ	0.610378	1.000000
Muanza	ascat	1.000000	0.672091
Muanza	in-situ	0.672091	1.000000

Use Spearman correlation when the relationship between your time series is not necessarily linear but generally moves in the same direction (monotonic). Spearman is great for data where the ranking of values is important and is less affected by outliers and non-normal distributions. This makes it a robust choice for various types of data. It’s also easy to interpret because it focuses on the overall trend.

df_combined.groupby("name").corr(method="spearman")

		ascat	in-situ
name
Buzi	ascat	1.000000	0.649886
Buzi	in-situ	0.649886	1.000000
Chokwé	ascat	1.000000	0.598663
Chokwé	in-situ	0.598663	1.000000
Mabalane	ascat	1.000000	0.758615
Mabalane	in-situ	0.758615	1.000000
Mabote	ascat	1.000000	0.739968
Mabote	in-situ	0.739968	1.000000
Muanza	ascat	1.000000	0.591772
Muanza	in-situ	0.591772	1.000000

Nevertheless, the correlation coefficients for both Pearson and Spearman methods range between 0.6 and 0.8 across different locations, indicating moderate to high positive correlations between the ASCAT HSAF 6.25\(\,\)km data and the in-situ soil moisture estimates. As a final step, we can visualize these correlation analyses using hvplot.

hvplot.scatter_matrix(df_combined.reset_index(level=0), c="name", alpha=0.3).opts(
    plot_size=300
)

Here, we observe that the relationship between in-situ and remotely sensed values is not entirely linear. Additionally, it indicates that soil moisture data is generally not normally distributed.

11.7 Scale of Measurement

We can only speculate about the reasons for these discrepancies, but it is important to note that the scale of in-situ measurements, which cover several centimeters around the device, compared to the averaged soil moisture value obtained by ASCAT, which encompasses about 50\(\,\)km\(^2\), might be a significant factor in explaining these differences. One can wonder what an averaged signal over such a broad area encompasses, as it can include a range of geomorphological, hydrological, and geological settings. Additionally, weather patterns can be confined to scales smaller than this area.

Rühlmann, M. Körschens, and J. Graefe, A new approach to calculate the particle density of soils considering properties of the soil organic matter and the mineral matrix, Geoderma, vol. 130, no. 3, pp. 272-283, Feb. 2006, doi: 10.1016/j.geoderma.2005.01.024.↩︎