import numpy as np
import xarray as xr
import matplotlib.pyplot as plt
import hvplot.xarray # noqa
import holoviews as hvIn this notebook, we aim to demonstrate how C-band (4–8 GHz, wavelengths of approximately 3.75–7.5 cm) and L-band (1–2 GHz, wavelengths of approximately 15–30 cm) radio frequencies differ for different land covers and times of the year. In addition, we’ll look at co- and cross-polarized backscattering:
- Sentinel-1 (C-band)
- VV
- VH
- ALOS-2 (L-band):
- HH
- HV
5.1 Data Loading
This is the same dataset as we created in the previous notebooks of exercise 4. If you did not manage to finish exercise 4 then you can find the dataset on this location ~/shared/datasets/rs/alos/ex5/fused_ds.zarr.
fused_ds = xr.open_dataset(
"fused_ds.zarr", engine="zarr", decode_coords="all", chunks={}
)The loaded data contains the Leaf Area Index (LAI), which is used as an estimate of foliage cover of forest canopies. So high LAI is interpreted as forested area, whereas low values account for less vegetated areas (shrubs, grass-land, and crops).
First we’ll have a look at the mean and standard deviation of LAI over all timeslices. This can be achieved by using the mean and std methods of the xarray object and by supplying a dimension over which these aggregating operations will be applied. We use the dimension “time”, thereby flattening the cube to a 2-D array with dimensions x and y.
fig, ax = plt.subplots(1, 2, figsize=(15, 6))
LAI_dc = fused_ds.LAI
LAI_mean = LAI_dc.mean("time")
LAI_std = LAI_dc.std("time")
LAI_mean.plot(ax=ax[0], vmin=0, vmax=6).axes.set_aspect("equal")
LAI_std.plot(ax=ax[1], vmin=0, vmax=3).axes.set_aspect("equal")
plt.tight_layout()/home/mschobbe/Documents/teaching/notebooks/microwave-remote-sensing/.conda_envs/mrs-env/lib/python3.11/site-packages/dask/array/numpy_compat.py:57: RuntimeWarning: invalid value encountered in divide
x = np.divide(x1, x2, out)
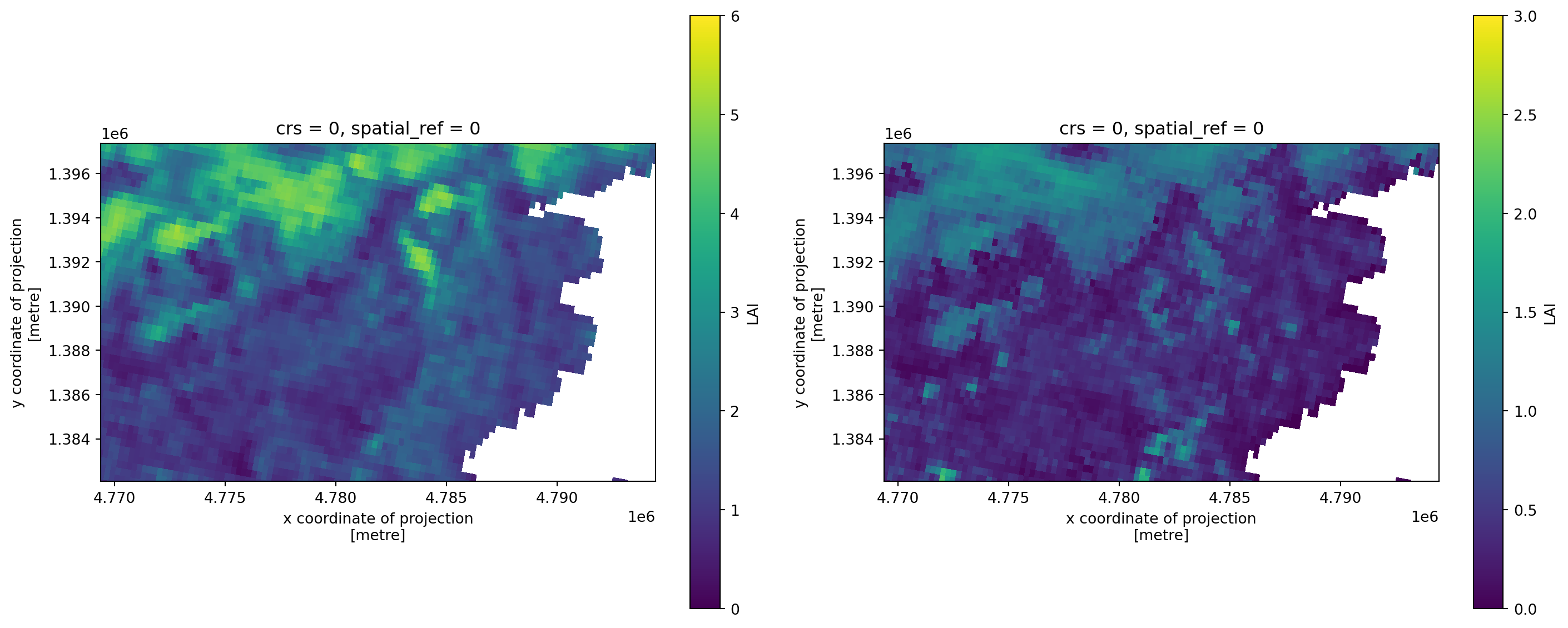
Figure 1: Map of mean LAI (left) and the associated standard deviation (right) for each pixel over time around Lake Garda.
It appears that the northern parts of our study area contain more and variable amounts of green elements per unit area. This might indicate a more complete coverage of foliage and thus forest.
5.2 Timeseries
Now that we have detected possible forested areas, let’s delve a bit deeper into the data. Remember that we deal with a spatiotemporal datacube. This gives us the possibility to study changes for each time increment. Hence we can show what happens to LAI for areas marked with generally low values as well as high values. We can achieve this by filtering the datacube with the where method for areas marked with low and high mean LAI values. In turn we will aggregate the remaining datacube over the spatial dimensions (“x” and “y”) to get a mean values for each time increment.
fig, ax = plt.subplots(1, 2, figsize=(15, 4))
LAI_low = LAI_dc.where(LAI_mean < 4)
LAI_high = LAI_dc.where(LAI_mean > 4)
LAI_low.mean(["x", "y"]).plot.scatter(x="time", ax=ax[0], ylim=(0, 6))
LAI_high.mean(["x", "y"]).plot.scatter(x="time", ax=ax[1], ylim=(0, 6))
ax[0].set_title("Low Mean LAI ($\\bar{LAI} < 4$)")
ax[1].set_title("High Mean LAI ($\\bar{LAI} > 4$)")
plt.tight_layout()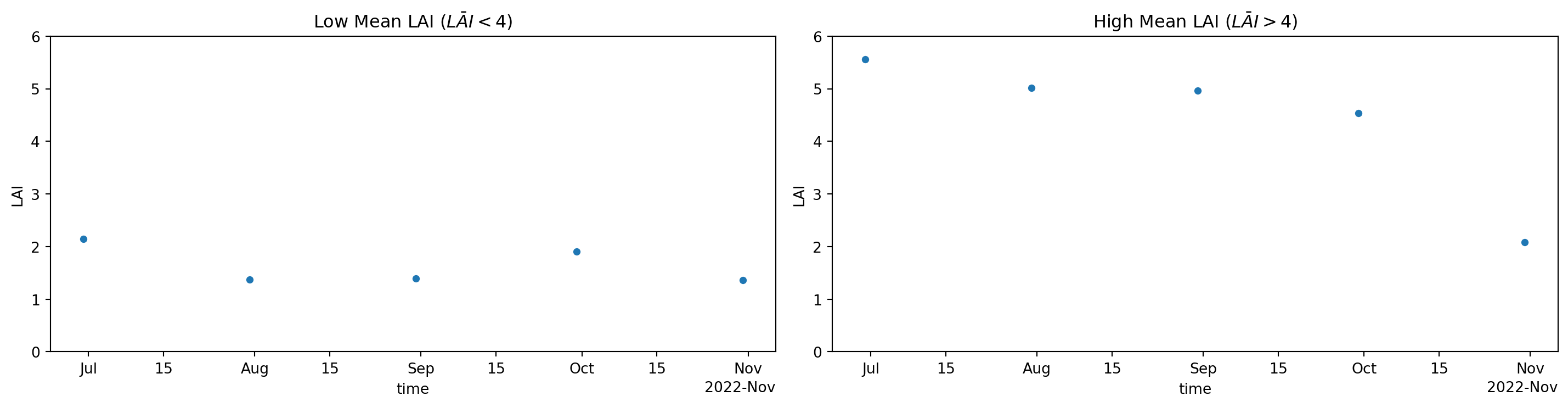
Figure 2: Timeseries of mean LAI per timeslice for areas with low (left) and high (right) mean LAI of Figure1.
Now we can see that areas with high mean LAI values (Figure 1) show a drop-off to values as low as those for areas with low mean LAI during the autumn months (Figure 2 ; right panel). Hence we might deduce that we deal with deciduous forest that becomes less green during autumn, as can be expected for the study area.
Remember that longer wavelengths like L-bands are more likely to penetrate through a forest canopy and would interact more readily with larger object like tree trunks and the forest floor. In turn, C-band microwaves are more likely to interact with sparse and shrub vegetation. The polarization of the emitted and received microwaves is on the other hand dependent on the type of backscattering with co-polarization (HH and VV) happening more frequently with direct backscatter or double bounce scattering. Whereas volume scattering occurs when the radar signal is subject to multiple reflections within 3-dimensional matter, as the orientation of the main scatterers is random, the polarisation of the backscattered signal is also random. Volume scattering can therefore cause an increase of cross-polarized intensity.
Let’s put this to the test by checking the microwave backscatter signatures over forested and sparsely vegetated areas as well as water bodies (Lake Garda). Let’s first look at the different sensor readings for the beginning of summer and autumn.
hv.output(widget_location="bottom")
t1 = fused_ds.gam0.\
isel(time=2).\
hvplot.image(robust=True, data_aspect=1, cmap="Greys_r",
rasterize=True, clim=(-25, 0)).\
opts(frame_height=400, aspect="equal")
t2 = fused_ds.gam0.\
isel(time=-1).\
hvplot.image(robust=True, data_aspect=1, cmap="Greys_r",
rasterize=True, clim=(-25, 0)).\
opts(frame_height=400, aspect="equal")
t1 + t2Figure 3: Maps of Sentinel-1 and ALOS-2 \(\gamma^0_T \,[dB]\) for the beginning of summer (left) and autumn (right).
The most notable difference is the lower energy received for cross-polarized than for co-polarized microwaves for both Sentinel-1 and ALOS-2. The latter differences are independent of the time of year. However, one can also note small changes in the received energy for the same satellite dependent on the time of year. To get a better feel for these changes over time we generate the following interactive plot. On the following plot one can select areas of a certain mean LAI (by clicking on the map) and see the associated timeseries of \(\gamma^0_T\) for each of the sensors.
LAI_image = LAI_mean.hvplot.\
image(rasterize=True, cmap="viridis", clim=(0, 6)).\
opts(title="Mean LAI (Selectable)", frame_height=400, aspect="equal")
def get_timeseries(x, y):
"""
Callback Function Holoviews
Parameters
----------
x: float
numeric value for x selected on LAI map
y: float
numeric value for y selected on LAI map
"""
lai_value = LAI_mean.sel(x=x, y=y, method="nearest").values
if np.isnan(lai_value):
select = fused_ds.where(LAI_mean.isnull())
label = "Water"
else:
mask = np.isclose(LAI_mean, lai_value, atol=0.05)
select = fused_ds.where(mask)
label = "Mean LAI: " + str(np.round(lai_value, 1))
time_series = (
select.gam0.to_dataset("sensor")
.median(["x", "y"], skipna=True)
.hvplot.scatter(ylim=(-30, 5))
.opts(title=label, frame_height=400)
)
return time_series
point_stream = hv.streams.SingleTap(source=LAI_image)
time_series = hv.DynamicMap(get_timeseries, streams=[point_stream])
LAI_image + time_seriesWARNING:param.RasterPlot01204: Due to internal constraints, when aspect and width/height is set, the bokeh backend uses those values as frame_width/frame_height instead. This ensures the aspect is respected, but means that the plot might be slightly larger than anticipated. Set the frame_width/frame_height explicitly to suppress this warning.Figure 4: Map of MEAN LAI around Lake Garda. The pixel values can be seen by hovering your mouse over the pixels. Clicking on the pixel will generate the timeseries for the associated mean LAI on the right hand-side. (Right) Timeseries of for Sentinel-1 and ALOS-2 \(\gamma^0_T [dB]\).
Can you see some patterns when analysing the different wavelengths and polarizations?
Remember again that we deal with a logarithmic scale. A measurement of 10 dB is 10 times brighter than the intensity measured at 0 dB, and 100 times brighter at 20 dB. The most notable difference is that the offset between cross- and co-polarised signals becomes larger at low LAI and lower at higher LAI. This might indicate the effect of volume scattering in forested areas where co- and cross-polarisation render backscattering values more equal. You will study the differences among cross- and co-polarized backscattering in more detail in the homework exercise.